2022. 6. 8. 20:33ㆍ2022-1/인공지능
1) 불확실성?(Uncertainty)
불확실한 지식이나 정보를 가지고도 올바른 결정을 내릴 수 있어야 함
불확실성이 나타나는 요인
- 데이터의 불확실성
- 지식의 불완전성
- 전문가들의 관점이 다른 경우
- 정보 획득의 불완전성
인공지능 시스템에서의 불확실성 처리
믿음의 정도 -> 확률 이론
불확실성을 처리하는 대표적인 방법
- 베이즈 추론(Bayesian reasoning)
- 확신도(certainty factor)
확률을 이용한 불확실성 처리
확률적인 추론(probabilistic reasoning)
-> 0.0에서 1.0 사이의 확률값을 가짐, 가장 확률이 높은 결론이 선택됨
2) 확률
확률의 기본 개념
확률: 특정한 사건(event)이 발생하는 비율
-> [0,1] 사이의 값으로 표현 (0: 불가능한 사건, 1: 확실한 사건)
상호배타적(mutually exclusive) 사건
-> 동시에 일어날 수 없는 사건
두 사건 A, B가 있을 때,
-> A가 일어난 일이 B가 일어나는 확률에 영향을 주지 않으면, B는 A와 독립(independent)
-> A가 일어난 일이 B가 일어나는 확률에 영향을 주면, B는 A에 종속(dependent)
사전 확률과 사후 확률
- 두 사건 A, B가 있고 사건 A와 B가 상호 배타적이지 않다고 가정
- 하나의 사건이 다른 사건의 확률에 영향을 준다고 가정
- 사건 B가 발생했을 때, 사건 A가 발생할 확률 (조건부 확률)

3) 베이즈 추론
베이즈 규칙(Bayes Rule)
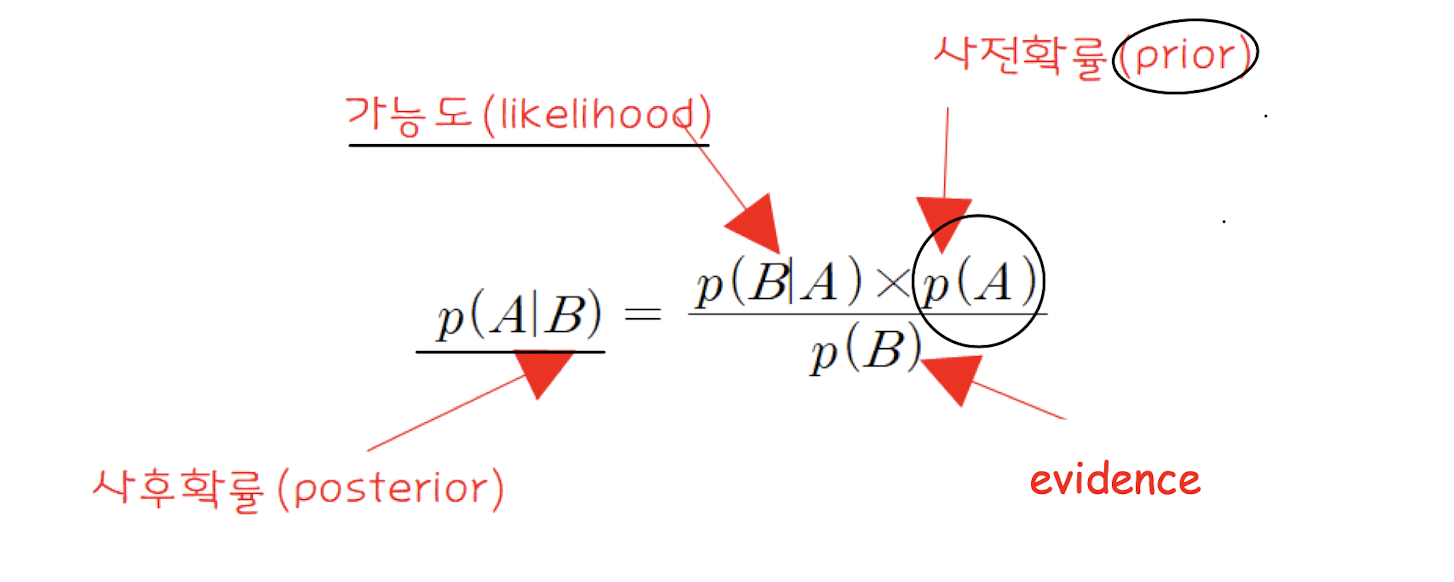
베이즈 정리 (Bayes Theorem)
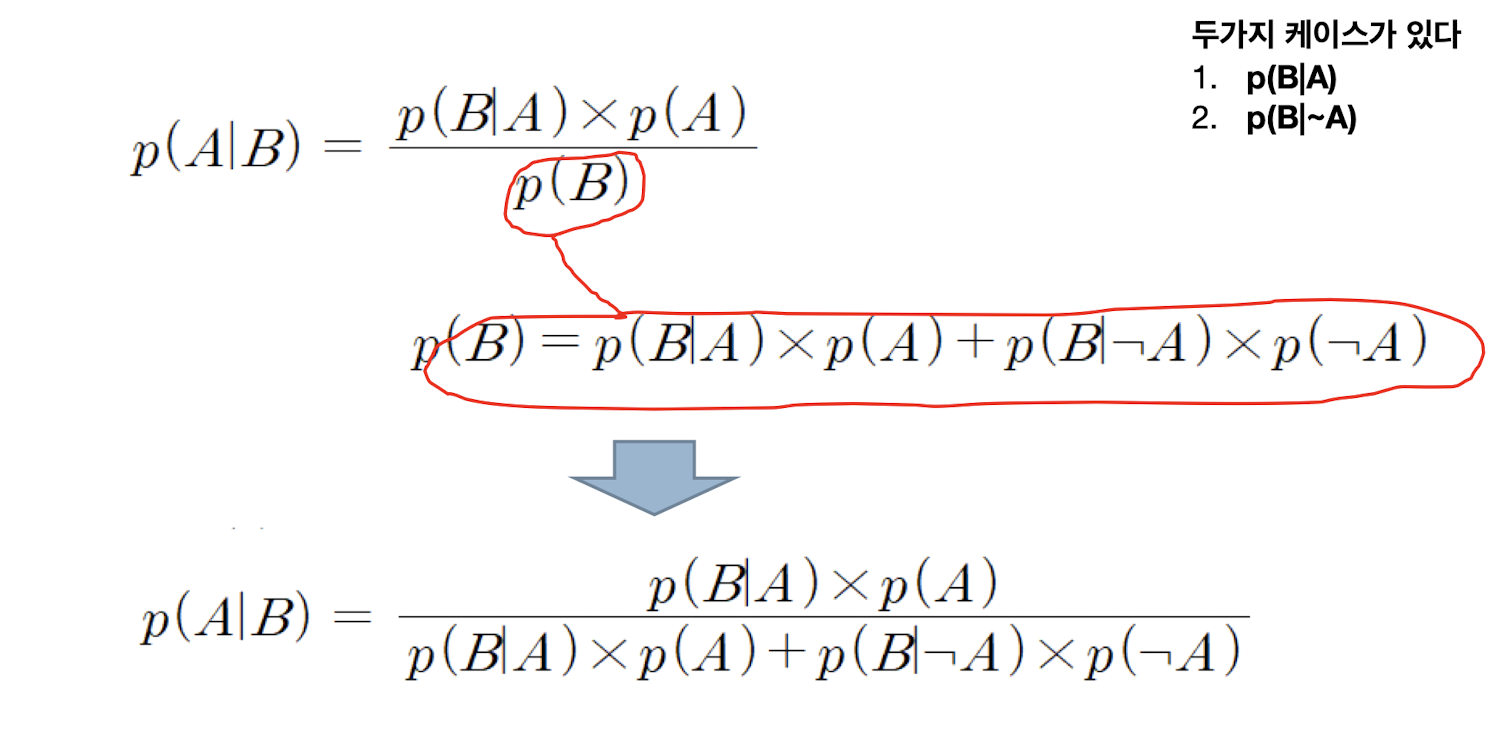
Lab: 과일 문제


Lab: 카드 게임


베이즈 정리와 추론


사전 확률과 가능도는 누가 제공?
-> 전문가들이 제공해야 함!

증거와 가설이 여러 개일 때

베이즈 정리의 단점
베이즈 추론이 정확한 결과를 도출하려면, 사전 확률 등의 확률값이 입력되어야 함
=> 기계학습 분야에서는 학습데이터로부터 자동 계산 혹은 학습
- 학습데이터로부터 사전 확률 계산
- 가능도에 대한 확률분포함수를 가정하고, 파라미터 학습
어떤 분야에서는 믿을만한 통계 자료가 없어서 사전확률을 산정할 수 없는 경우도 있음 ex) 의학 분야
Lab: 베이즈 정리로 규칙의 확률 계산

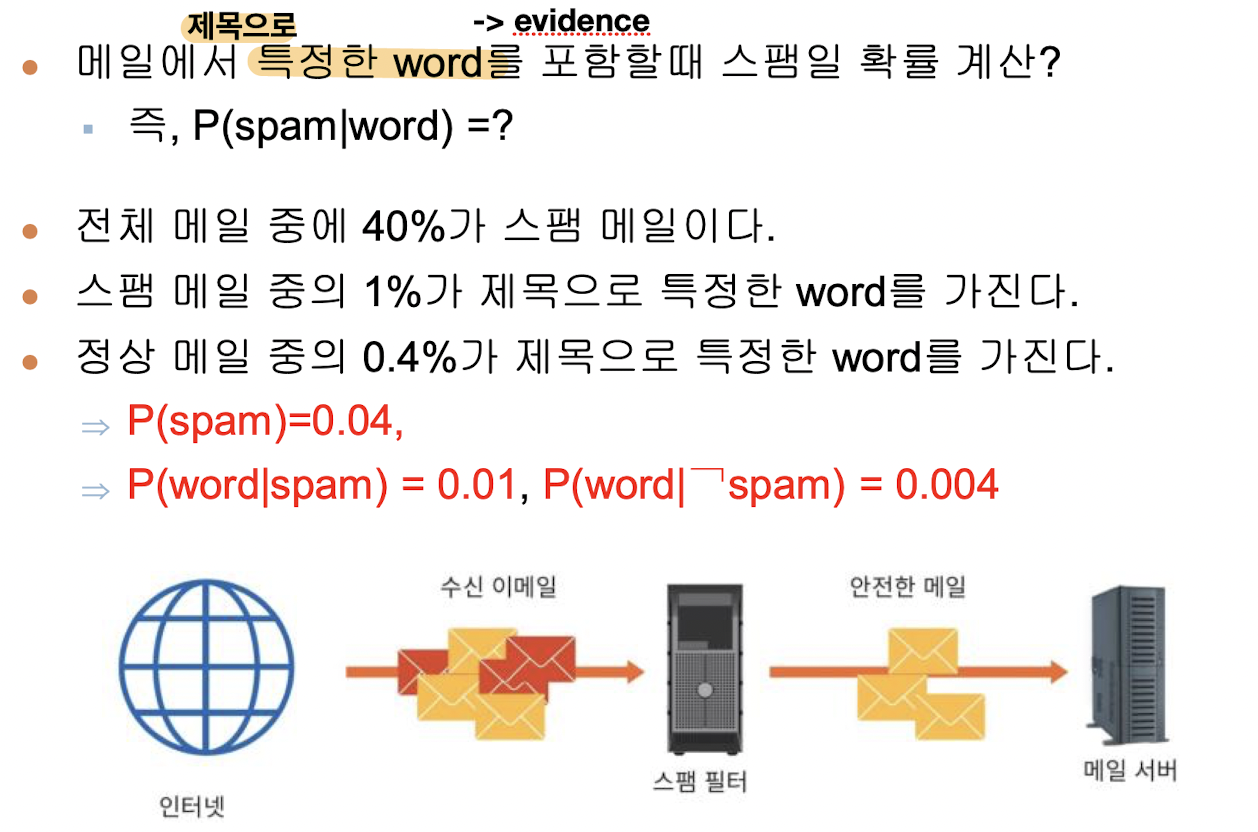
Lab: 스팸 필터링

Lab: Z-바이러스


4) 확신도(Certainty Factor)
확신도는 MYCIN에서 사용 (MYCIN: 박테리아 감염 진단, 치료하는 전문가 시스템)
베이즈 추론의 대안으로 사용 (확률 이론을 사용하기 위해서는, 너무 많은 조건부 확률이 필요)
=> 확률추정에 필요한 데이터 확보 어려움
=> 대안으로 확신도라는 수치를 도입
확신도(cf)란 전문가가 특정사실에 대해 가지는 신뢰도 수치
- -1.0~+1.0의 값을 가짐
- -1.0 값은 확실한 거짓, +1.0 값은 확실한 참을 의미
전문가의 언어적 표현을 직관적 수치로 표시, 확률과 별개

확신도의 정의
규칙의 증거가 가설을 얼마나 강력하게 지원하는지를 나타냄

어떤 규칙이 점화되기 위해서는 확신도가 문턱값(threshold)을 넘어야 함, 이때 불신의 정도인 MD가 영향을 심하게 끼치게 됨.
=> 단점 방지하기 위해 확신도의 정의를 변경함
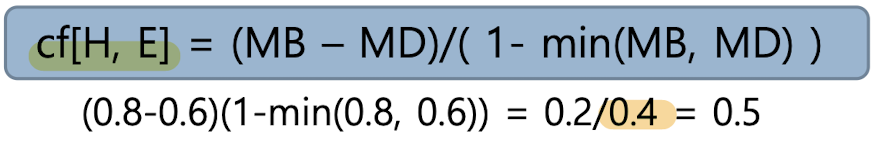
확신도의 전파

불확실한 증거를 가진 경우의 확신도

규칙이 여러 개의 전제를 가지는 경우


Summary

'2022-1 > 인공지능' 카테고리의 다른 글
| [인공지능] 10장 선형 회귀 (0) | 2022.06.09 |
|---|---|
| [인공지능] 9장 기계학습 (0) | 2022.06.09 |
| [인공지능] 6. 퍼지논리 (1) | 2022.04.15 |
| [인공지능] 5. 지식 표현 (0) | 2022.04.15 |
| [인공지능] 4. 전문가 시스템 (0) | 2022.04.15 |