2022. 4. 15. 16:14ㆍ2022-1/인공지능
1. 퍼지 논리란?
fuzzy의 정의 - "not clear, distinct, or precise; blurred", 애매하거나 모호함을 의미
퍼지 논리란?
-명확하게 정의될 수 없는 지식을 표현하는 방법
-ex) 비가 약간 오면, 수문을 조금만 개방한다
* 애매한 논리가 아니라, 애매함을 표현할 수 있는 논리
=> 애매함을 다루는 질서정연한 논리
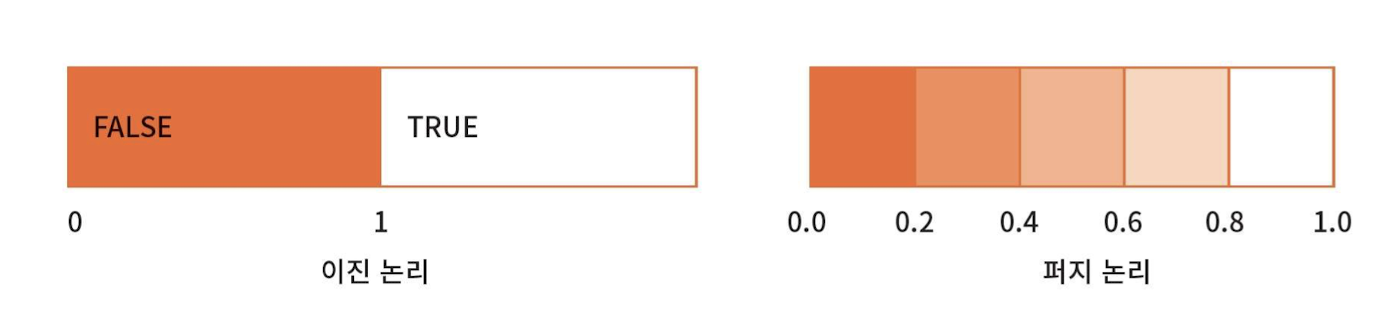
이진 논리 vs 퍼지 논리
이진 논리(Boolean Logic)
-참과 거짓(즉, 1 or 0)의 진리값만을 가짐: 흑백논리
퍼지 논리
-[0.0,1.0] 범위의 진리값을 가진다.
-인간이 사용하는 지식 표현의 애매성을 해결할 방법이 필요
-1965년 Zadeh에 의해 퍼지 집합에 관한 이론이 처음 제시
-퍼지 명제나 규칙을 다루기 위한 퍼지 논리로 발전


기존의 이진 논리가 참/거짓의 2개의 값만을 나타낼 수 있다
퍼지논리는 multi-valued logic
퍼지 논리의 사용 가능 분야
주로 제어 분야에 많이 사용




퍼지 논리와 집합
퍼지 논리와 집합 이론은 매우 밀접한 관련이 있다
-이진 논리 == 기존 집합 (Crisp set, 크리스프 집합)
-퍼지 논리 == 퍼지 집합
기존의 집합
A={7,8,9}
-원소는 집합에 속하거나 속하지 않음
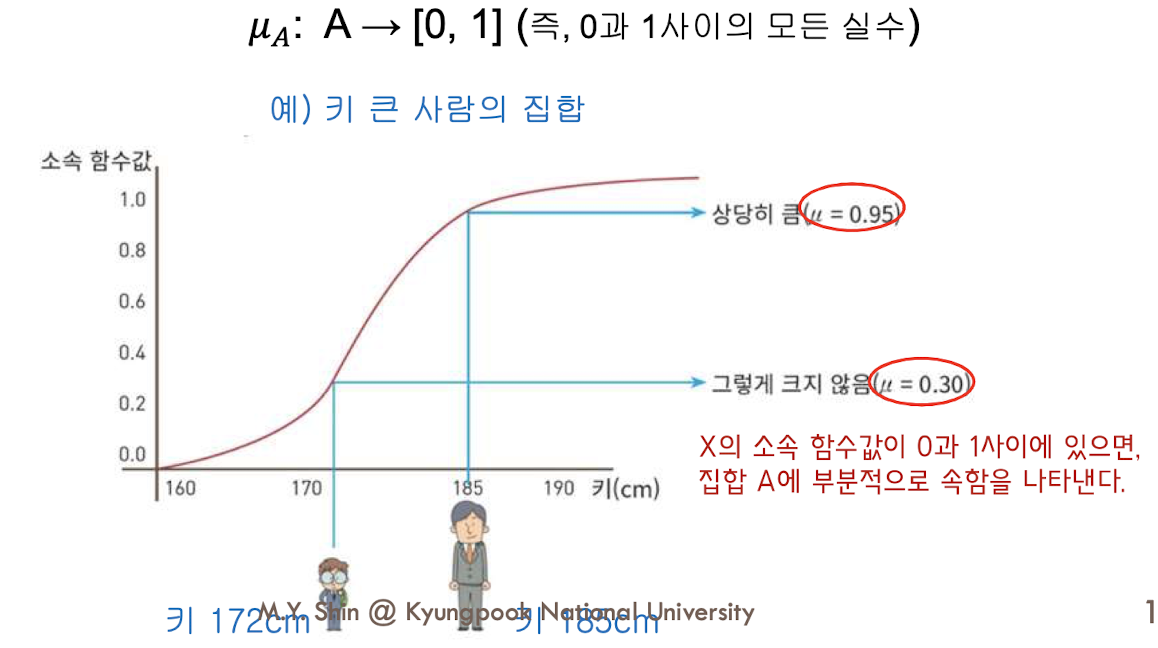
-소속 함수(Membership Function)로 표현하면 다음과 같다.

-즉, 이 소속 함수는 집합 A의 원소를 {0,1}에 대응시킴
2. 크리스프 집합과 퍼지 집합
크리스프 집합(Crisp Set)
집합에 속하거나 속하지 않는 두 가지 경우만 존재

퍼지 집합
어떤 원소가 집합에 속하는지 속하지 않는지를 단정적으로 다루지 않음
원소가 집합에 속하는 정도에 따라 소속 함수값을 0과 1 사이의 값으로 대응
크리스프 집합 vs 퍼지 집합
크리스프 집합: 경계가 분명한 집합
퍼지 집합: 경계가 분명하지 않은 집합
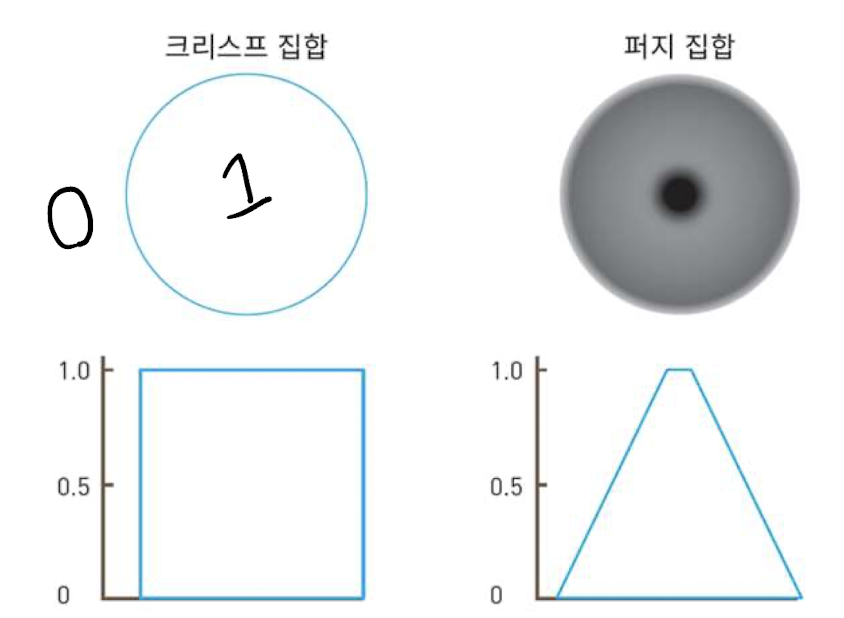

크리스프 집합은 퍼지 집합안에 속해 있다고 볼 수 있다 그렇기에 퍼지 집합은 크리스프 집합을 표현할 수 있다.
퍼지 집합의 표기 방법
비연속적인 퍼지 집합의 경우
-각 원소의 소속 함수값을 다음 과 같이 두 가지 형태로 표기 가능
1. 집합 A={소속함수값/원소,...}의 형태로 표기
*여기서 "/"는 나눗셈 표시가 아니라 원소의 소속함수값을 분리시키는 표시
2. 집합 A={(원소, 소속함수값),(..),...}의 형태로 표기

연속적인 퍼지집합의 경우
-소속 함수값을 함수로 표시하여야 함

퍼지 집합의 예

3. 퍼지 집합에서의 연산자
논리 연산자 사용이 가능

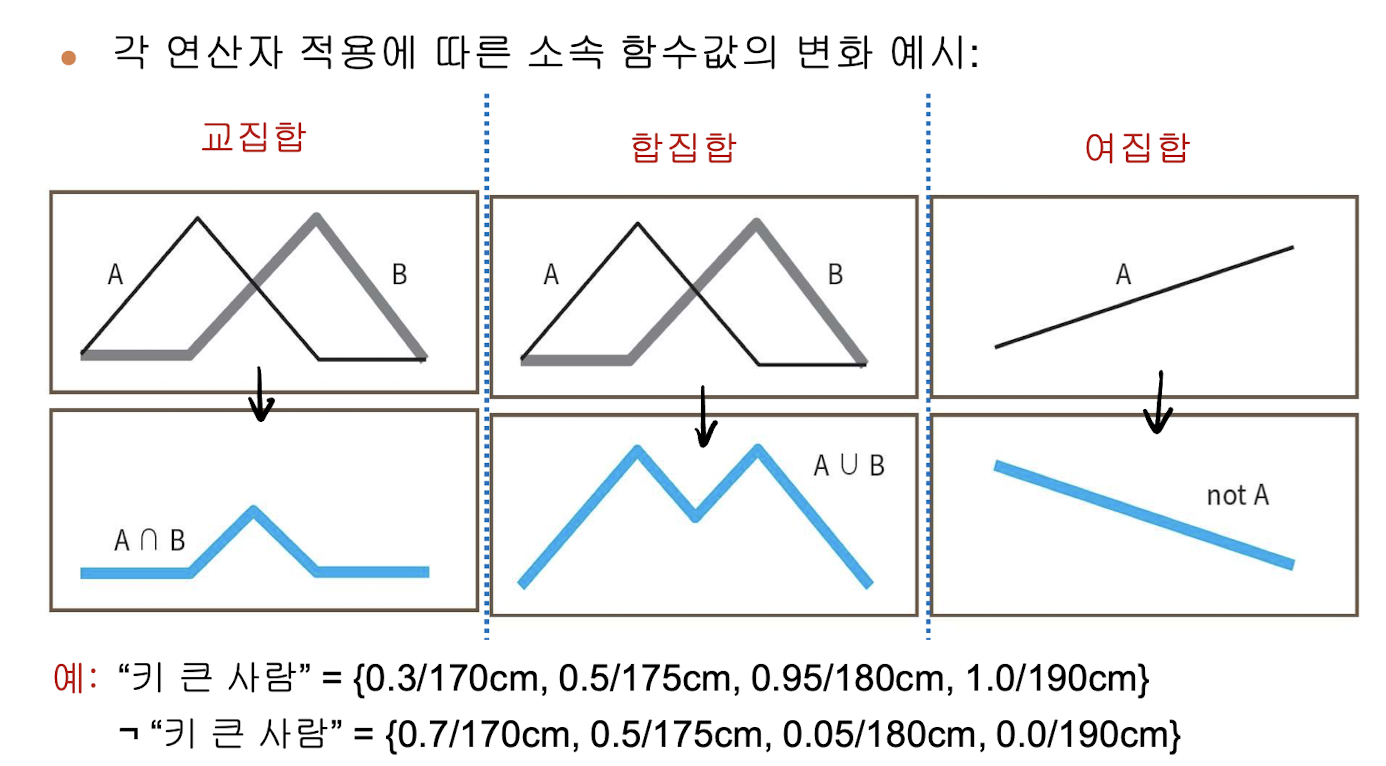
합집합

교집합

여집합

크리스프 집합에서의 연산자와 비교
크리스프 집합은 퍼지집합에 속하기 때문에, AND OR NOT 게이트의 경우에는 연산자를 취했을 때도 똑같은 결과가 나옴

연산자 CON과 DIL
연산자 CON(Concentration) - 집중 연산
-소속 함수값의 제곱을 계산하는 연산자

-"매우"라는 수식어를 추가할 때 사용

연산자 DIL(Dilation)- 확장 연산, CON과 반대되는 연산자
-소속 함수값의 제곱근을 계산하는 연산자
-"약간"이라는 수식어를 추가할 때 사용

4. 퍼지 추론

"기존의 이진 논리보다 추론 확장이 가능하다"
퍼지 규칙
1973년 자데 교수는 인간의 지식을 퍼지 규칙으로 표현할 것을 제안
퍼지 규칙이란?
IF x가 A
THEN y는 B
여기서 x,y는 언어변수
A,B는 x,y의 퍼지 집합에서 결정된 언어값


modus ponens

퍼지 추론 방법
1. 규칙의 전제(IF 부분)를 평가하는 단계
2. 규칙의 결론(THEN 부분)을 적용(혹은 함축)하는 단계
-Cf. 고전적인 규칙 기반 시스템: 규칙의 전제가 참이면 결론도 참,
퍼지 시스템에서, 전제가 소속함수값(소속도) 정도로 참이면, 결론도 소속함수값(소속도) 정도로 참이다
퍼지 추론 과정

추론 과정
(1) 입력 단계: 센서로부터 입력되는 값을 소속 함수값으로 매핑(입력 변수의 퍼지화, fuzzification)
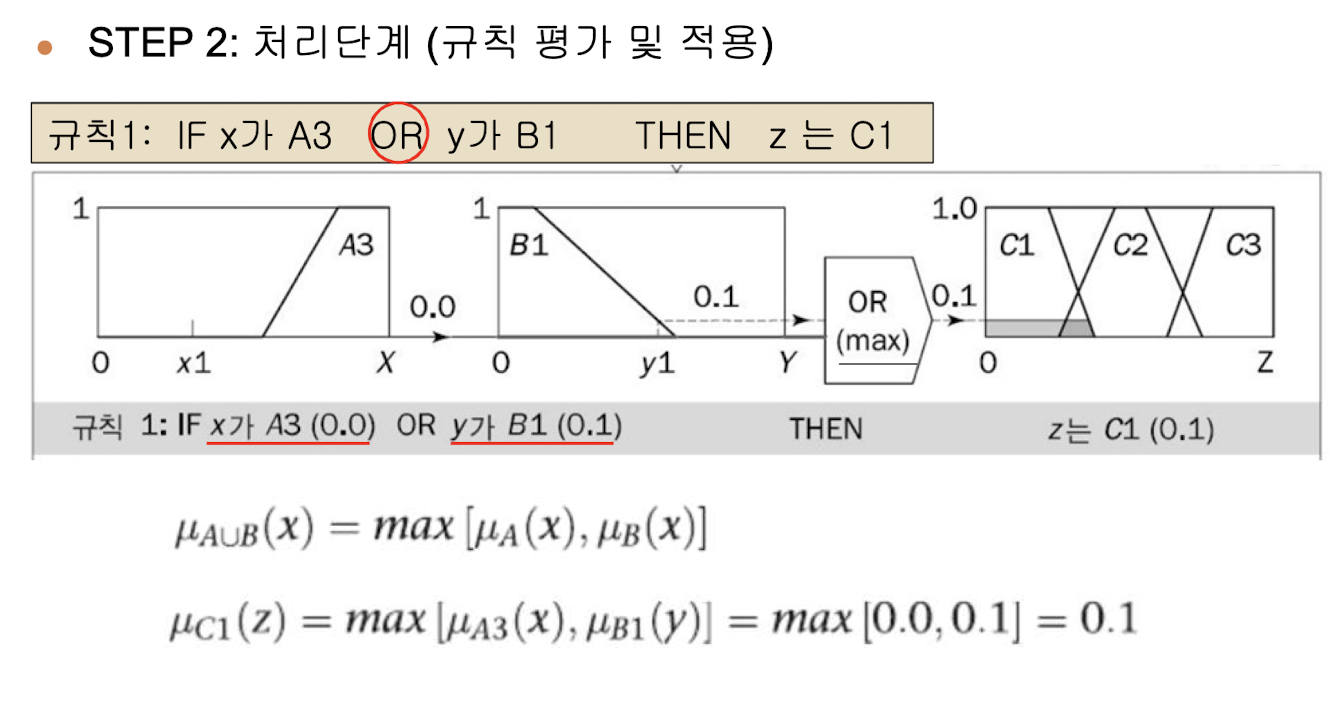
(2) 처리 단계: 추론엔진이 적절한 규칙들을 점화하여 각 규칙들에 대한 결과 생성 후 규칙 결과 결합
(3) 출력 단계: 결합된 규칙 결과를 특정 출력값으로 변환 (역퍼지화, defuzzification)
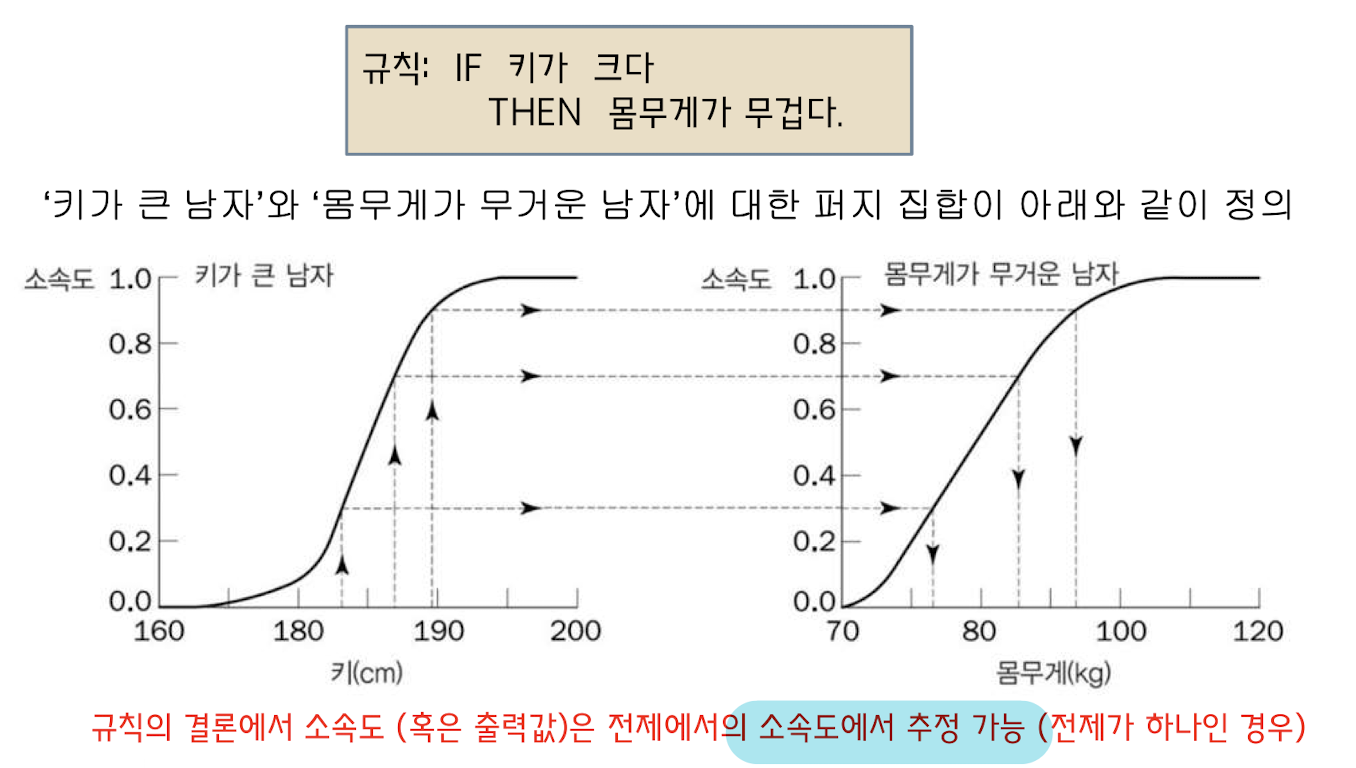
EX: 퍼지 규칙의 전제가 여러 개인 경우




규칙이 여러개일 때







LAB: 팁을 주는 문제



'2022-1 > 인공지능' 카테고리의 다른 글
| [인공지능] 9장 기계학습 (0) | 2022.06.09 |
|---|---|
| [인공지능] 7장 불확실성 (0) | 2022.06.08 |
| [인공지능] 5. 지식 표현 (0) | 2022.04.15 |
| [인공지능] 4. 전문가 시스템 (0) | 2022.04.15 |
| [인공지능] 3. 게임트리 (0) | 2022.04.15 |