[Machine Learning-Andrew ng ] 1주차 - Lecture 2 Model and Cost Function 강의 노트

Model Representation

가장 간단한 학습 알고리즘인 선형 회귀(Linear Regression)에 대해서 알아보자 

m은 training example의 개수, 이 예시에서는 47개의 학습 예제를 가지고 있어서 m은 47개이다!

x는 특징(feature)라고 부루는 입력 변수

y는 출력 값이나 예측하려하는 목표변수

 

그래서 (x,y)는 하나의 학습예제를 표기할 것임

ex) (x^(1), y^(1)) : (2104,460) 여기서 ^(1)은 표기상 그렇게 표현한 것이고, i번째 임을 의미하는 것이지 i제곱이 아니다!

 

 

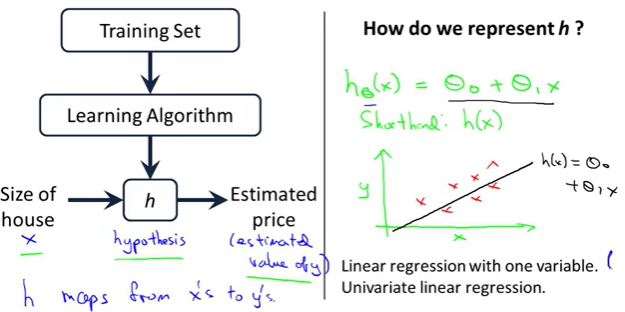
위의 그림과 같은 예시에서, size of house가 x(feature)이고 Extimated price가 y(목표변수)일 것이다

그래서 x의 선형함수인 y를 예측하는 가설 h를 표현하기 위해서 여기서는 선형함수를 사용한다

비선형 함수를 사용해도 괜찮지만, 간단한 선형함수 부터 살펴보자. 여기서

그래서 다음과 같은 식을 생성한다. 이 모형을 하나의 변수로 생성된 형태이기 때문에 단일변량 선형회귀라고 부를 수 있다. 그럼 이제 어떻게 이모델을 실행시킬지 살펴보자

 

Cost Function

그렇다면 이전의 h(x)에서 두개의 파라미터 세타0,세타1을 어떻게 고를까?

위의 사진과 같은 데이터 분포와 가장 유사하게 나타나도록 파라미터 값을 선택해야 할 것임

즉 h(x)와 y간의 차이를 최대한 작게 만들어야 할 것이다.

이것을 수학적으로 표현하면 error = h(x) -y가 최솟값을 갖는 것이 좋을 것이다.

근데 error 값이 음수일 수도 있고, 양수일 수도 있기 때문에 error 값의 합을 바로 구하는 것은 적합하지 않다.

그래서 제곱값의 합을 구하여 그 합이 최소가 되는 parameter를 찾는 방법이 일반적 이를 LSE(least squared error) 라고 한다.

 

그래서 가설 함수 h(x)를 cost function을 사용해서 정확도를 측정하게 되는 것인데

이 cost function은 mean square error(MSE)인데, error^2의 평균이 cost 값이 된다. 

여기서 m으로 나누지 않고, 2m으로 나누었다는 점이 다른데 2는 계산상의 편의를 위한 것으로 나중에 확인 할 것이다.

 

intution 1

 

우리의 목표는 이전에 설명했듯이 J를 최소화 시키는 파라미터 값을 찾는 것이다

일단 직관적인 이해를 위해 세타0는 0이라고 가정하고

를 찾자

 

 

그래서 세타1이 1일 때 J(세타1)을 구해보면 값이 0이 나오는 것을 확인 할 수 있다.

 

 

세타1이 0.5일 때도 찾아보자.

무수히 많은 세타1의 값을 찾아보면 

밑의 합수와 같이 그래프를 생성할 수 있고

global minimum 세타1을 찾을 수 있다!

intution 2

만약에 파라미터 값이 두개라면 다음과 같은 3차원 형태가 그려질 것이다

 

이 함수에서 크기를 색상으로 표현하여

2차원 평면에 나타나면 등고선 모양이 된다.

이제 우리는 cost function J(세타)가 최소값을 갖도록 하는 parameter를 구하고 싶을 것이다!

이를 자동으로 구하는 방법은 다음 장에서 다룬다.